扩增子数据分析之多样性指数: alpha多样性
多样性指数(Diversity index)和计算公式可以见: wikipedia
Alpha多样性(Alpha Diversity)是对某个样品中物种多样性的分析,包含样品中的物种类别的多样性——丰富度(Richness)和物种组成多少的整体分布——均匀度(Evenness)两个因素,通常用Richness,Chao1,Shannon,Simpson,Dominance和Equitability等指数来评估样本的物种多样性。
丰富度指数
Richness, Chao1,Shannon三个指数是常用的评估丰富度的指标,数值越高表明样品包含的物种丰富度就越高。
Richness指数: 指样本中被检测到的OTU量;
Chao1指数 : 通过低丰度OTUs来进一步预测样品中的OTUs数量;
Shannon指数 : 计算考虑到样品中的OTUs及其相对丰度信息,
通过对数(如以2为底的shannon_2,以自然对数为底的shannon_e
以10为底的shannon_10)转换来预测样品中的分类多样性。
均匀度指数
Simpson,Dominance和Equitability三个指数是常用的评估均匀度的指标。
Simpson指数 : 表示随机选取两条序列属于同一个分类(如OTUs)的概率(故数值在0~1之间),
数值越接近1表示表明OTUs的丰度分部越不均匀;
Dominancez指数 : 取值为1-Simpson,表示随机选取两条序列属于不同分类(如OTUs)的概率;
Equitability指数: 根据Shannon指数值计算,当其值为1时表明样品中的物种丰度分布绝对均匀,
而其值越小这表明物种丰度分布呈现出越高的偏向。
汇总表:
| 指数 | 单位 | 计算方式 |
|---|---|---|
| richness | OTUs | 样本中至少包含一条序列的OTU数目 |
| chao1 | OTUs | N + S^2 / (2D^2),其中N为OTU个数, S为丰度为1的OTUs个数,D为丰度为2的OTUs数目; |
| shannon_2 | bits | sum(f), 对所有OTU频率计算p*log(p,2)和, p为OTU的频率; |
| shannon_e | nats | sum(f), 对所有OTU频率计算p*log(p,e)和, p为OTU的频率; |
| shannon_10 | dits | sum(f), 对所有OTU频率计算p*log(p,10)和, p为OTU的频率; |
| simpson | Probability | sum(f^2), f为所有OTU频率的和 |
| dominance | Probability | 1-simpson |
| equitability | shannon/log(N), N为OTU数(logs to base 2) |
实例:
USEARCH alpha_div
USEARCH 提供了alpha_div函数进行计算各种指数, 可通·-metrics 指定需要计算指数,支持的指数有: berger_parker、buzas_gibson、chao1、dominance、equitability、jost、jost1、reads、richness、robbins、simpson shannon_e、shannon_2、shannon_10
usearch -alpha_div otutable.txt -output alpha.txt
usearch -alpha_div otutable.txt -output gini.txt -metrics gini_simpson
usearch -alpha_div otutable.txt -output alpha.txt -metrics chao1,
QIIME diversity alpha
qiime2 数据分析流程通过 qiime diversity接口提供了分析`alpha多样性·的各种命令:
--i-table : FeatureTable
--p-metric : enspie|michaelis_menten_fit|strong|lladser_pe|fisher_alpha
|goods_coverage|doubles|simpson|margalef|observed_otus|osd
|shannon|pielou_e|chao1|brillouin_d|menhinick|simpson_e
|kempton_taylor_q|robbins|dominance|lladser_ci|heip_e
|singles|chao1_ci|mcintosh_d|ace|mcintosh_e|gini_index
|berger_parker_d|esty_ci
--o-alpha-diversity: 输出alpha多样性;
--output-dir: 输出目录(如不指定--o-distance-matrix);
执行:
qiime diversity alpha \
--i-table table.qza \
--p-metric goods_coverage \
--o-alpha-diversity goods_coverage.qza
https://rdrr.io/cran/otuSummary/man/alphaDiversity.html
Invsimpson – mothur
Biological diversity - the great variety of life !
在探索simpson指数之前,我们需要理解几个很重要的概念:
生物多样性可以用很多种方式定量,其中两个主要的因素是丰富度(richness)和均匀度(evenness)。
1. Richness
丰富度即每个样本的物种数,样本中物种越多,样本越“丰富”。
物种丰富度从概念上讲,并不考虑(样本中)每个物种有多少个个体。它给于个体数少的物种与个体数多的数种相同的权重。因此,在某地区1朵雏菊与1000朵金凤花对丰富度的影响是一样的。
2. Evenness
均匀度即不同物种的相对丰度(abundance),它与丰富度互相补充,相辅相成(make up)。
[译者注] 这里其实有三个概念:Richness, Evennes 和abundance。例如A组:类1有3个,类2有5个,类3有6个;B组:类1有4个,类2有4个,类3有4个。那么A组有3类,B组也有3类,所以它们的richness是一样的;A组中3个类所含个体数均不相同,而B组中3个类所含个体数相同,因此A组和B组的evennes不同;A组类1有3个,B组类1有4个,所以就类1而言B组的abundance更高。
我们对两个地区不同的野花进行取样,以此为例。第1个地区包括300朵雏菊,335朵蒲公英和365朵金凤花。第2个地区包括20朵雏菊,49朵蒲公英和931朵金凤花,如下表。两个样本丰富度相同(均有3个物种),总的个体数也相同(均为1000朵)。然而第1个地区样本的均匀度比第2个地区样本的均匀度更高。这是因为(在第1个地区)3个物种个体分布较均匀,第2个地区大多数是金凤花,仅有少数雏菊和蒲公英。因此认为样本2比样本1的多样性更低。
相比于由相似丰度的许多物种组成的群落,由一两个优势物种组成的群落具有更低的多样性。
多样性随物种丰富度和均匀度的增加而增加。Simpson指数兼顾丰富度和均匀度。
Simpson多样性指数实际上涉及三个相似的指数:
Simpson’s Index (D)
它反映的是在同一个样本中随机的抽取2个个体,这两个个体来自同一个类的概率。有以下两个版本的公式来计算simpson指数。两者不矛盾,均可接受。
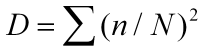 |
 |
| n = the total number of organisms of a particular species N = the total number of organisms of all species |
|
D值在0-1之间。0表示无限多样,1表示没有多样性。也就是说D值越大,多样性越低。这与直觉和逻辑不符,为了解决这个问题,通常会用1减去D:
Simpson’s Index of Diversity 1-D
这个值也在0-1之间,但是此时,值越大多样性越高,这就变得更直观了。这种情况下,指数代表的意义是在同一个样本中随机的抽取2个个体,这两个个体来自不同类的概率。
对于违背直觉的D值,还有另一种处理办法,即用1除以D:
Simpson’s Reciprocal Index 1 / D
1/D的最小值为1。当它为1时表示样本仅由1个物种组成。值越大,多样性越高。最大值是样本中的物种数。例如,假设一个样本中有5个物种,则1/D的最大值为5。
[译者注] 当样本中这5个物种的丰度都相等时1/D达到最大值5。大家可以通过求二阶偏导来求出极值,因非本文重点,证明从略。
以上三个指数想用哪一个取决于使用者的分析需求,但是在研究中需指明使用哪一个指标作为simpson指数![译者注:该文作者着重强调了这一点,请注意!]
# ====================== 译文结束 =======================
这篇材料提供的案例很好,但是遗憾的是仅说明了simpson指数与evennes关系。为了进行单因素比较,作者将两组丰富度设为相同。那么如果丰富度不同呢?而且simpson指数是否与shannon指数一样与丰度无关呢?这里再举一个例子(因为各组相互独立,这里就不给生物学意义,直接上数字了,具体可查看另一篇shannon指数博文[2]):
A组:2, 4, 6, 8
B组:20, 40, 60, 80
C组:5, 5, 5, 5
D组:5, 5, 5, 5, 5
代入公式1-D计算(因为微生物16SrRNA经典流程QIIME使用的scikit库是利用这个公式计算的〔3〕),我们可以得出:
A组simpson指数为: 1-((2/20)^2+(4/20)^2+(6/20)^2+(8/20)^2) = 0.7
A组shannon指数为 1.846439(计算公式见博文[2],下同)
B组simpson指数为: 1-((20/200)^2+(40/200)^2+(60/200)^2+(80/200)^2) = 0.7
B组shannon指数为 1.846439
C组simpson指数为: 1-((5/20)^2)*4 = 0.75
C组shannon指数为 2.0
D组simpson指数为: 1-((5/25)^2)*5 = 0.8
D组shannon指数为 2.321928
从上面的计算过程很明显看出A组和B组相等,C组和D组不相等,A组和C组也不相等。
AB组结果相同显示出在丰富度一致时simpson指数与丰度无关,它只与相对丰度(均匀度)有关。这和shannon指数一致,归根结底是因为公式中自变量都是相对丰度pi!
CD组结果不同显示出在均匀度一致时simpson指数与丰富度有关,丰富度越大,simpson指数越小。这一点也和shannon指数的情况一致,归根结底,原因在于公式中都有加和项,而且加和部分无论是simpson指数的(pi)2还是shannon指数的x*log2(x)在区间(0,1〕上均大于0(有关x*log2(x)>0, x∈(0,1〕可以查看博文〔2〕中的y= – x*log2(x)那张图)。因此,无论是shannon指数还是simpson指数每多加一项(即丰富度增加),值都会越来越小。回到抽样上来讲,当样本中每种个体数都相同时,在一个样本中随机抽取两个个体,种类越多抽到的这两个个体来自同一个种类的概率越大。
AC组显示出当丰富度相同时,样本中种类越均一,simpson指数越大,即种类越均一,随机抽取两个个体属于同一个种类的概率越大。这一点可以查看博文〔2〕中的分析过程。对应shannon指数的y = – x*log2(x), simpson指数的y = – x2 在(0,1〕间区上,也是一个斜率逐渐减小的单调递减函数。
综上,simpson和shannon指数都是均匀度和丰富度的综合指标。
〔1〕 http://www.countrysideinfo.co.uk/simpsons.htm


Recent Comments